¿Qué Son las Permutaciones en Probabilidad? Descubre su Definición y Ejemplos Clave

Introducción a las Permutaciones

¿Alguna vez te has preguntado cuántas maneras diferentes puedes organizar un grupo de elementos? ¡Eso es precisamente lo que estudian las permutaciones! Las permutaciones son una herramienta matemática fascinante que nos permite explorar las diferentes formas en que podemos disponer un conjunto de objetos. Imagina que tienes un grupo de amigos y quieres sentarlos en una mesa; la manera en que los organizes puede cambiar completamente la dinámica del grupo. Pero, ¿cómo se calcula cuántas formas hay de hacerlo? Aquí es donde entran las permutaciones. En este artículo, vamos a desglosar este concepto, dándote una comprensión clara y ejemplos que te harán ver las permutaciones de una manera nueva y emocionante.

¿Qué Son las Permutaciones?

Las permutaciones son simplemente diferentes maneras de organizar un conjunto de elementos. Por ejemplo, si tienes tres letras: A, B y C, las permutaciones serían ABC, ACB, BAC, BCA, CAB y CBA. En total, hay seis formas diferentes de organizar estas letras. Pero, ¿cómo llegamos a ese número? La fórmula básica para calcular permutaciones es P(n) = n!, donde n! (n factorial) es el producto de todos los números enteros desde 1 hasta n. Así que, en nuestro ejemplo, 3! = 3 × 2 × 1 = 6.

La Importancia de las Permutaciones

Entender las permutaciones es fundamental en el campo de la probabilidad y la estadística. No solo se aplican a situaciones cotidianas como organizar amigos, sino que también son cruciales en áreas como la criptografía, donde el orden de los elementos puede cambiar el significado de un mensaje. Además, en la teoría de juegos, las permutaciones nos ayudan a analizar las diferentes estrategias que los jugadores pueden emplear. ¡Así que la próxima vez que pienses en cómo organizar algo, recuerda que estás en el mundo de las permutaciones!

Ejemplos Prácticos de Permutaciones

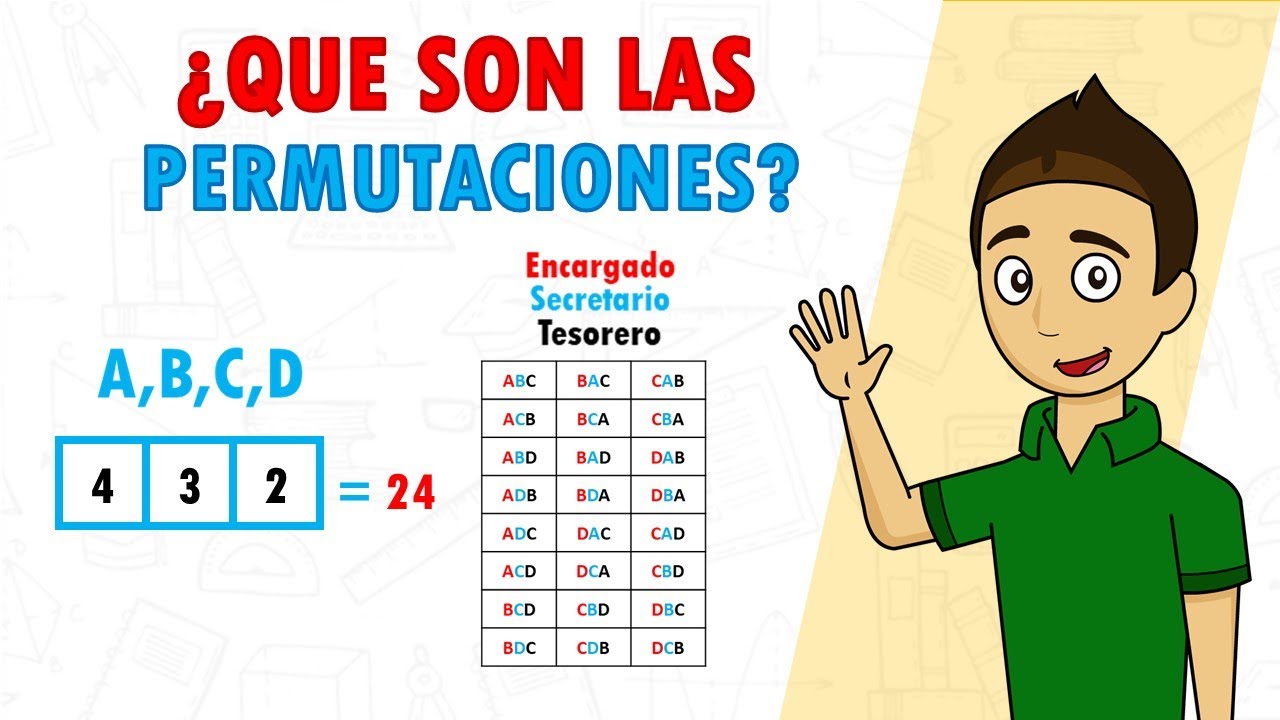
Para entender mejor las permutaciones, veamos algunos ejemplos prácticos. Imagina que estás organizando un pequeño concurso de talentos entre tus amigos. Tienes cuatro amigos: Ana, Luis, Marta y Pedro. ¿Cuántas maneras diferentes puedes organizarlos para que se presenten en el escenario?

Usando la fórmula de permutaciones, calculamos 4! = 4 × 3 × 2 × 1 = 24. Así que hay 24 formas diferentes de organizar a tus amigos. Puedes imaginarte todas las diferentes combinaciones y cómo cada una podría cambiar la energía del evento. ¿No es emocionante pensar en ello?

Permutaciones con Repetición

Pero, ¿qué pasa si algunos de tus amigos tienen talentos similares? Por ejemplo, si Ana y Marta son ambas cantantes y Luis y Pedro son magos, la situación cambia. Aquí es donde entran las permutaciones con repetición. Si tienes un conjunto de elementos donde algunos se repiten, la fórmula cambia a P(n; n1, n2, ... nk) = frac{n!}{n1! × n2! × ... × nk!}, donde n es el total de elementos y n1, n2, ... nk son las repeticiones.

Si volvemos a nuestro ejemplo, donde Ana y Marta son cantantes, y Luis y Pedro son magos, tendríamos 4 elementos en total, pero 2 de ellos son cantantes. Entonces, el cálculo sería P(4; 2, 2) = frac{4!}{2! × 2!} = frac{24}{2 × 2} = 6. ¡Eso significa que hay 6 maneras diferentes de organizar a tus amigos considerando sus talentos!

Aplicaciones de las Permutaciones en la Vida Real

Las permutaciones no son solo un concepto abstracto que se queda en el aula. Tienen aplicaciones prácticas en muchas áreas de la vida real. Por ejemplo, en el mundo de la música, los compositores a menudo utilizan permutaciones para crear variaciones de una melodía. Cada vez que reorganizan las notas, están creando una nueva pieza musical. También en la planificación de eventos, como mencionamos antes, las permutaciones ayudan a los organizadores a determinar el mejor orden para que los participantes se presenten.

Permutaciones en Juegos de Azar

Además, las permutaciones son fundamentales en juegos de azar. Imagina que estás jugando a un juego de cartas y tienes que barajar un mazo. La forma en que barajas las cartas determina el orden en que aparecerán. En este caso, el número de permutaciones puede ser extremadamente grande, lo que garantiza que cada juego sea único. Si tienes un mazo de 52 cartas, el número de maneras en que puedes organizar esas cartas es 52!, que es un número astronómico.

Cómo Calcular Permutaciones de Manera Efectiva

Calcular permutaciones puede parecer complicado al principio, pero con un poco de práctica se vuelve más sencillo. Aquí hay algunos pasos que puedes seguir:

• Identifica el número total de elementos: Antes de empezar a calcular, asegúrate de saber cuántos elementos tienes en total.
• Determina si hay repeticiones: Si algunos de los elementos se repiten, recuerda que tendrás que usar la fórmula de permutaciones con repetición.
• Aplica la fórmula: Usa la fórmula correspondiente y realiza los cálculos necesarios.

Ejemplo de Cálculo Paso a Paso

Supongamos que quieres organizar una carrera de tres corredores: Juan, Carla y Pedro. Aquí, no hay repeticiones, así que usamos la fórmula básica:

1. Identificamos que hay 3 corredores.
2. Aplicamos la fórmula: P(3) = 3! = 3 × 2 × 1 = 6.
3. Las diferentes maneras de organizarlos son: Juan-Carla-Pedro, Juan-Pedro-Carla, Carla-Juan-Pedro, Carla-Pedro-Juan, Pedro-Juan-Carla, y Pedro-Carla-Juan.

¡Y ahí lo tienes! Seis maneras diferentes de organizar la carrera.

Preguntas Frecuentes sobre Permutaciones

1. ¿Las permutaciones son lo mismo que las combinaciones?

No, las permutaciones y las combinaciones son conceptos diferentes. Las permutaciones se centran en el orden de los elementos, mientras que las combinaciones solo se ocupan de la selección de elementos sin importar el orden.

2. ¿Cuándo debo usar permutaciones en lugar de combinaciones?

Debes usar permutaciones cuando el orden de los elementos es importante. Por ejemplo, en una carrera, el primer lugar, segundo lugar y tercer lugar son distintos, por lo que debes considerar las permutaciones.

3. ¿Cómo se relacionan las permutaciones con la probabilidad?

Las permutaciones son fundamentales para calcular probabilidades en situaciones donde el orden es relevante. Ayudan a determinar cuántas maneras diferentes pueden ocurrir ciertos eventos, lo que es crucial para calcular probabilidades.

4. ¿Qué pasa si tengo un número muy grande de elementos?

Cuando trabajas con un número grande de elementos, los cálculos pueden volverse complicados. Sin embargo, muchas calculadoras y software matemáticos pueden ayudarte a calcular permutaciones de manera rápida y eficiente.

5. ¿Puedo aplicar permutaciones en la vida diaria?

¡Absolutamente! Las permutaciones se aplican en muchas situaciones cotidianas, como organizar eventos, planificar rutas, y en juegos y deportes. Cualquier momento en el que el orden de los elementos importe, las permutaciones están en juego.

En resumen, las permutaciones son un concepto poderoso que nos ayuda a entender y organizar el mundo que nos rodea. Ya sea que estés organizando un evento, jugando un juego o simplemente tratando de resolver un rompecabezas, las permutaciones pueden ofrecerte una nueva perspectiva. Así que la próxima vez que te enfrentes a un conjunto de elementos, ¡recuerda la magia de las permutaciones!