Clasificación de las Funcciones en Cálculo Diferencial: Guía Completa para Estudiantes

Introducción a la Clasificación de Funciones

¿Alguna vez te has preguntado cómo se clasifican las funciones en el cálculo diferencial? Si es así, ¡estás en el lugar correcto! Las funciones son como el corazón del cálculo; sin ellas, no tendríamos muchas de las herramientas que utilizamos para entender el mundo matemático que nos rodea. Imagina que cada función es un camino en un vasto paisaje. Algunos caminos son rectos y sencillos, mientras que otros son sinuosos y complicados. En este artículo, vamos a explorar las diferentes clasificaciones de funciones, cómo se comportan y cómo se relacionan entre sí. Así que, prepárate para un viaje fascinante a través del mundo de las funciones.

¿Qué es una Función?

Antes de sumergirnos en la clasificación de las funciones, es fundamental entender qué es una función. En términos simples, una función es una relación entre dos conjuntos, donde a cada elemento del primer conjunto (llamado dominio) le corresponde exactamente un elemento del segundo conjunto (llamado codominio). Piensa en una máquina expendedora: introduces una moneda (entrada) y seleccionas un producto (salida). Esa relación es lo que hace que las funciones sean tan interesantes y útiles.

Clasificación de Funciones

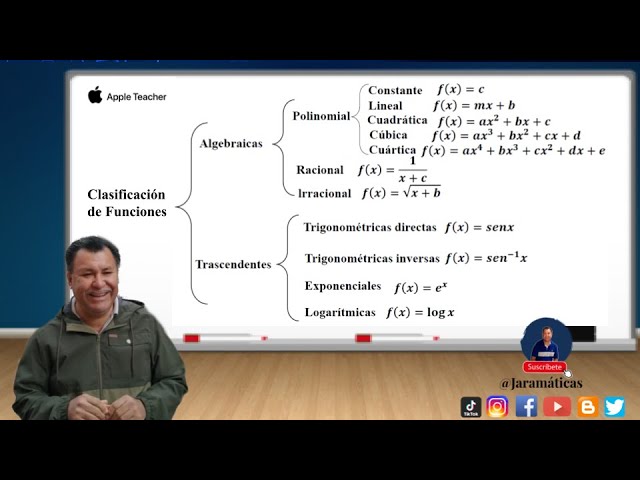
Ahora que tenemos una idea básica de lo que es una función, hablemos de cómo se clasifican. Las funciones pueden clasificarse de varias maneras, y cada clasificación nos da información valiosa sobre su comportamiento. Las clasificaciones más comunes incluyen:

1. Funciones Algebraicas

Las funciones algebraicas son aquellas que se pueden expresar mediante polinomios. Esto significa que se componen de términos que incluyen variables elevadas a potencias enteras no negativas. Un ejemplo clásico de función algebraica es (f(x) = x^2 + 3x + 2). Estas funciones pueden ser muy simples, como una línea recta, o más complejas, como una parábola. ¡Es como tener una caja de herramientas! Dependiendo de lo que necesites, puedes elegir la herramienta adecuada para resolver un problema.

2. Funciones Trigonométricas

Las funciones trigonométricas, como seno, coseno y tangente, son fundamentales en el cálculo diferencial, especialmente cuando se trata de problemas relacionados con ángulos y ciclos. Imagina que estás en un parque de atracciones, y la rueda de la fortuna gira. La altura a la que te encuentras en la rueda puede describirse usando funciones trigonométricas. Estas funciones son periódicas, lo que significa que se repiten en intervalos regulares. Esto es extremadamente útil en el estudio de fenómenos que tienen un comportamiento cíclico, como las olas del mar o las estaciones del año.

3. Funciones Exponenciales y Logarítmicas

Las funciones exponenciales son aquellas en las que la variable aparece como un exponente. Un ejemplo clásico es (f(x) = e^x), donde (e) es la base del logaritmo natural. Estas funciones crecen muy rápidamente y son utilizadas en diversas áreas, como la biología para modelar el crecimiento poblacional. Por otro lado, las funciones logarítmicas son la inversa de las exponenciales. Así que, si la función exponencial es como una carrera a toda velocidad, la función logarítmica es como el regreso a casa, donde reflexionas sobre la distancia recorrida.

4. Funciones Racionales

Las funciones racionales son aquellas que se pueden expresar como el cociente de dos polinomios. Un ejemplo sería (f(x) = frac{x^2 + 1}{x – 1}). Estas funciones pueden presentar comportamientos interesantes, como asíntotas y discontinuidades. Imagina que estás conduciendo por una carretera; a veces, hay baches que te obligan a desacelerar. Las discontinuidades en las funciones racionales son esos baches en el camino matemático.

5. Funciones Irracionales

Las funciones irracionales incluyen raíces cuadradas, cúbicas y otras raíces de expresiones. Un ejemplo es (f(x) = sqrt{x}). Estas funciones pueden ser un poco más complicadas de manejar, especialmente cuando se trata de su dominio. Sin embargo, son esenciales en muchas aplicaciones, desde la física hasta la ingeniería. Piensa en ellas como esos acertijos que a veces parecen imposibles de resolver, pero que tienen una solución clara una vez que entiendes cómo funcionan.

Propiedades de las Funciones

Además de clasificarlas, también es importante conocer algunas propiedades clave de las funciones. Estas propiedades nos ayudan a entender mejor cómo se comportan y cómo interactúan entre sí.

1. Dominio y Rango

El dominio de una función es el conjunto de todos los posibles valores de entrada (x) que podemos usar. Por otro lado, el rango es el conjunto de todos los valores de salida (y) que la función puede producir. Imagina que estás en una fiesta y solo hay ciertas personas con las que puedes hablar (dominio), y de esas conversaciones, solo puedes obtener ciertas respuestas (rango). Conocer el dominio y el rango de una función es esencial para trabajar con ella.

2. Continuidad

Una función es continua si no hay saltos, interrupciones o agujeros en su gráfico. Piensa en un río que fluye sin obstáculos. Si encuentras un bache, eso significa que la función no es continua. La continuidad es crucial en el cálculo diferencial porque muchas de las técnicas que utilizamos requieren que las funciones sean continuas para poder aplicar reglas como la derivación.

3. Derivabilidad

La derivabilidad es otra propiedad importante que se relaciona con cómo cambia una función. Si una función es derivable, significa que podemos calcular su tasa de cambio en cualquier punto. Esto es como tener un velocímetro en tu coche: te dice cuán rápido estás yendo en un momento dado. Sin derivabilidad, no podríamos utilizar muchas de las herramientas del cálculo diferencial.

Aplicaciones de las Funciones en el Cálculo Diferencial

Las funciones no son solo un concepto abstracto; tienen aplicaciones prácticas en el mundo real. Desde la economía hasta la física, las funciones nos ayudan a modelar y entender situaciones complejas. Veamos algunas de estas aplicaciones.

1. Economía

En economía, las funciones se utilizan para modelar el comportamiento del mercado. Por ejemplo, la oferta y la demanda se pueden representar mediante funciones, lo que permite a los economistas predecir cómo cambiarán los precios en función de diferentes factores. Es como un juego de ajedrez; cada movimiento tiene una reacción y es importante anticiparse a los cambios.

2. Física

En física, las funciones son fundamentales para describir el movimiento. La posición de un objeto en el tiempo se puede expresar como una función, y al derivar esa función, podemos encontrar la velocidad y la aceleración. Imagina que estás lanzando una pelota al aire; la trayectoria de la pelota se puede modelar con funciones, y al calcular la derivada, puedes saber en qué momento alcanzará su altura máxima.

3. Biología

Las funciones también se utilizan en biología para modelar el crecimiento de poblaciones. El crecimiento exponencial es un concepto común en biología, y las funciones pueden ayudarnos a predecir cómo crecerá una población bajo ciertas condiciones. Es como cuidar un jardín; si no controlas el crecimiento, las plantas pueden desbordarse y competir entre sí por recursos.

Conclusiones

En resumen, las funciones son un pilar fundamental del cálculo diferencial y tienen un impacto profundo en diversas disciplinas. Desde su clasificación hasta sus propiedades y aplicaciones, entender las funciones te permitirá abordar problemas matemáticos y del mundo real con confianza. Así que, la próxima vez que te encuentres con una función, recuerda que es mucho más que una simple relación; es una herramienta poderosa que puede ayudarte a desentrañar los misterios de la matemática y la ciencia.

Preguntas Frecuentes

1. ¿Cuál es la diferencia entre una función continua y una función discontinua?

Una función continua no tiene saltos ni interrupciones en su gráfico, mientras que una función discontinua presenta al menos un punto donde no se puede trazar una línea continua.

2. ¿Por qué es importante conocer el dominio de una función?

Conocer el dominio de una función es crucial porque nos dice cuáles son los valores de entrada válidos. Sin esta información, podríamos intentar evaluar la función en puntos que no tienen sentido.

3. ¿Cómo se relacionan las funciones algebraicas con el cálculo diferencial?

Las funciones algebraicas son una de las formas más comunes de funciones que encontramos en el cálculo. Sus propiedades y comportamientos son esenciales para aplicar técnicas de derivación y entender cómo cambian.

4. ¿Qué papel juegan las funciones trigonométricas en el cálculo?

Las funciones trigonométricas son fundamentales en el cálculo, especialmente en problemas que involucran ángulos y ciclos, y son esenciales para entender fenómenos periódicos.

5. ¿Se pueden combinar diferentes tipos de funciones?

Sí, se pueden combinar diferentes tipos de funciones para crear funciones compuestas. Por ejemplo, puedes tener una función algebraica que incluye una función trigonométrica, lo que te permitirá modelar situaciones más complejas.